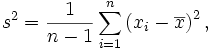Modelo de Regressão

Este descrever a relação entre uma variável explanatória 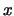e uma variável resposta 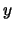. O modelo faz a seguintes suposições, em ordem decrescente de importância:

1. o valor médio da variável resposta é uma funçãi linear de ,
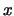2. a variância da variável resposta é constante (ou seja, a mesma para todos os valores de ),
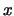3. a variação aleatória da variável resposta para qualquer valor fixo de 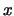segue uma distribuição Normal, e estes termos de erro são independentes.

Saber Saber mais: 

Variância Populacional

Em estatística, o conceito de variância também pode ser usado para descrever um conjunto de observações. Quando o conjunto das observações é uma população, é chamada de Variâcia Populacional.

Na prática, quando lidando com grandes populações, é quase sempre impossível achar o valor exacto da variância da população, devido ao tempo, custo e outras restrições aos recursos.

Um método comum de estimar a variância da população é através da tomada de amostras. Quando estimando a variância da população usando n amostras aleatórias x_i onde i = 1, 2, ..., n, a fórmula seguinte é um estimador não esperado:

 

 

 

Como Calcular a Variância Populacional?

Variância Amostral

Na teoria da probabilidade e na estatística, a variância de uma variável aleatóriaé uma medida da sua dipersão estatística, indicando quão longe em geral os seus valores se encontram do valor esperado.

Se μ = E(X) é o valor esperado, (média) da variável aleatória X.

 

Questões de Variância:

Medida de dispersão

Descrevem apenas uma das características dos valores numéricos de um conjunto de observações, o da tendência central. Porém, nenhuma delas informa sobre o grau de variação ou dispersão dos valores observados. Em qualquer grupo de dados os valores numéricos não são semelhantes e apresentam desvios variáveis em relação a tendência geral de média. 

As medidas de dispersão servem para avaliar o quanto os dados são semelhantes, descreve então o quanto os dados distam do valor central. Desse jeito, as medidas de dispersão servem também para avaliar qual o grau de representação da média.

 

Saber mais sobre a Medida de Dispersão.